5 Mesoscale: myofibrils and fibers
This chapter presents the challenges and preliminary contributions to the modeling of muscle contraction at the mesoscale. Regulation mechanisms in muscle contraction, in particular in the heart, operate at this scale. They are currently the object of an intense research activity, so the content of the chapter should be considered more as a perspective for future work than a presentation of past contributions.
5.1 Background: anatomy of a myofibril
5.1.1 Definition of the Mesoscale

The definition of the “mesoscale” is ambiguous. We recall that the molecular scale is the nanometer, and the size of the power-stroke conformational change is ~10 nm, see Chapter 1. The scale of the tissue is the cm . In this section, we present in more details the anatomic structure of muscle fibers and suggest a definition of what to call the mesoscale.
A longitudinal cut of a sarcomere is shown on Figure 5.1. The sarcomere is delimited by two Z-lines, and it is symmetric with respect to the M-line. The distance between two consecutive Z-lines is typically 2 μm. The A-bands are the regions where the myosin motors interact with the actin filament. The center H-zone corresponds to the region of the thick filament where there are no motors. The I-band is the region containing only actin filaments.
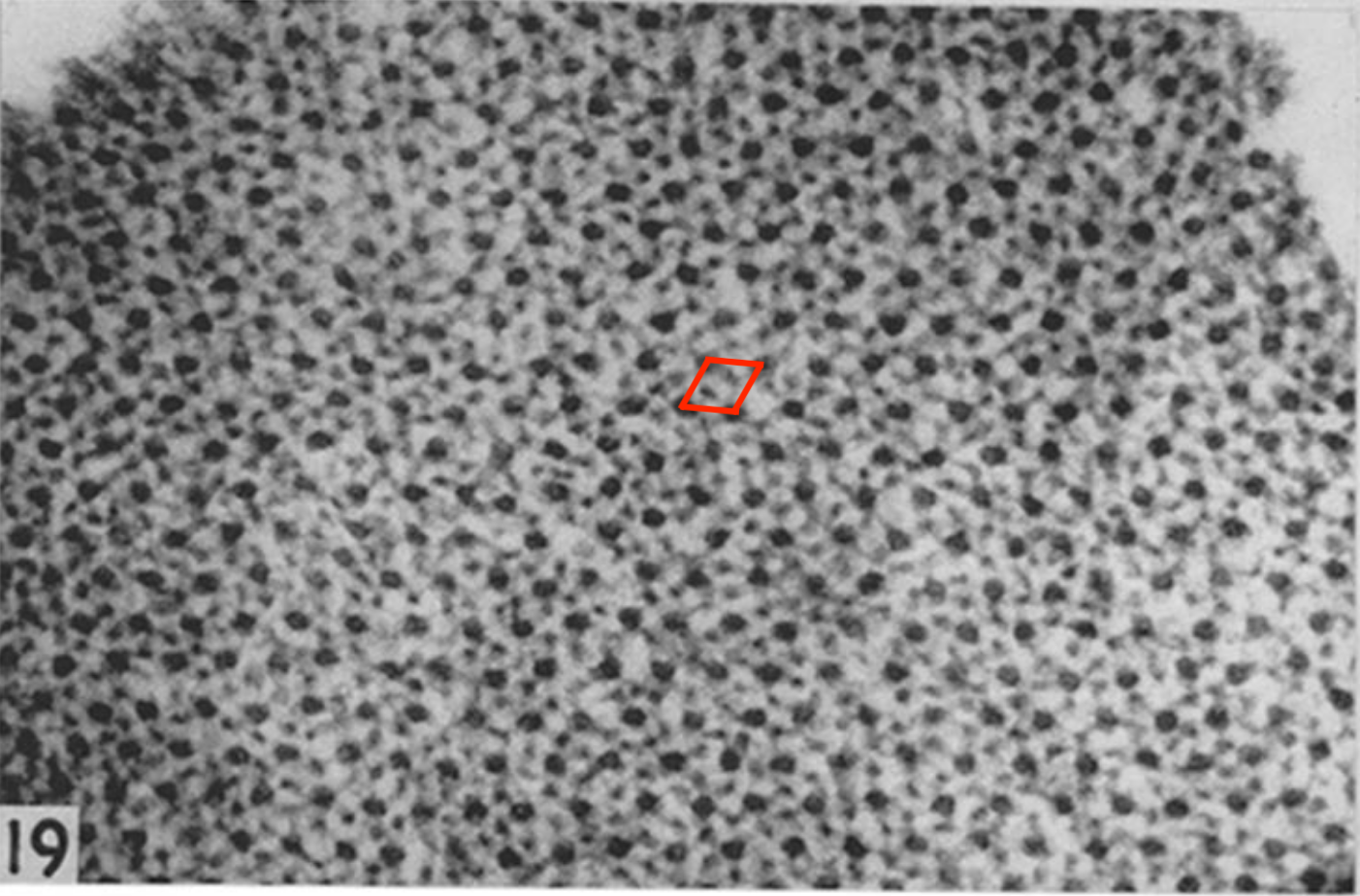
The cross-section of a sarcomere is a cristalline hexagonal lattice of thick and thin filaments, see Figure 5.2. The unit cell of the lattice containing one thick filament for two thin filaments is a contractile unit. The side of the unit cell being 40 nm, there are about 600 contractile units per sarcomere (Reconditi 2006).
Muscle fibrils (myofibrils) are successions of sarcomeres that span the whole length of a muscle cell, i.e. a few centimeters, and constitute the main component of its cytoplasm, see Figure 5.3. Their diameter is about 1 μm (Mobley and Eisenberg 1975). Each muscle cell (or fiber) contains about 104 myofibrls working in parallel. Muscle fibers are in turn bundled in fascicles which constitute the last step before the tissue scale. The typical diameter of a fascicle is 1 mm.

According to the above description, one could argue that the muscle tissue has seven scales: molecular motors, contractile units, sarcomeres, fibrils, cells, fascicles and tissue, so it is not clear which one can be considered as the most representative “mesoscale”.
From the point of view of activation, the representative unit is the cell, since it is at their membrane that the electric signal from the motor neurons is converted in to a chemical signal in the cytoplasm. It thus seems reasonable to “merge” the fiber (cells) and the fibrils scales into one. Both myofibrils and fibers and could be considered as slender continua, since their length is about 100 times to 1000 times larger than their diameter. The meso-scale structure could thus be defined as the elementary representative portion of this 1D continuum that would comprise a “sufficient” number of sarcomeres in the longitudinal direction.
The main assumption behing this representation is that the sarcomeres deforms uniformly within a representative volume element or that non-uniformities average out. This would excluse strong localized phenomena. The homogeneity of the sarcomere deformation within the representative volume element depends primarily on the properties of the strucutres that connects these sarcomeres both in the longitudinal and transverse directions. Another question is whether the friction between the fascicles has some effect on the macroscopic properties of the tissue. A more thorough litterature review is necessary to answer this second question.
Here, we choose to define the mesoscale as a representative set of contractile units that can serve as the basis of a 1D-homotenized model. One of the objective of the work on this scale will be to refine this definition and come up with an elementary representative volume.
5.1.2 Cytoskeletal structural elements
In this section, we provide a quick overview of experimental findings supporting the need for detailed modeling of the mesoscale muscle structures. The following does not constitute a complete review; it rather points at good entry points to establish a more thorough state of the art. For an overview of the sarcomeric molecular structure we refer in particular to the work of Craig and Padrón (2004) and Wang et al. (2021).
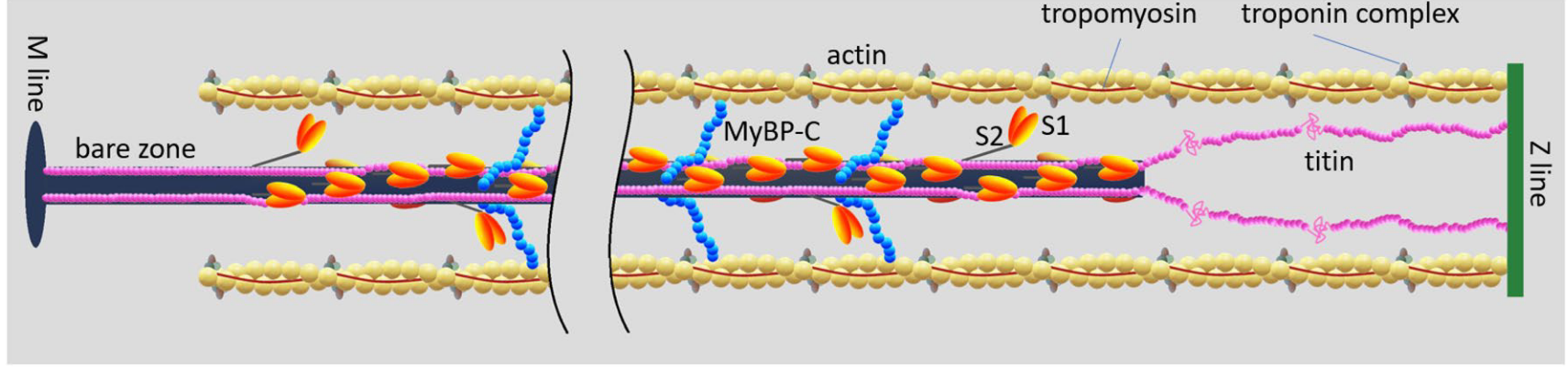
The elastic network connecting the contractile units together has essentially three elements: the M-lines, the Z-disks and the titin proteins,1 see Figure 5.4.
1 The Myosin Binding Protein C (MyBP-C) is a protein that connects the thick and thin filament within the sarcomere. Its function is still not fully understood, but it may play a fundamental role in the regulation of muscle contraction, see (Heling, Geeves, and Kad 2020; Henderson et al. 2017). Its elastic properties do not seem to be known.
- Z-disks (also called Z-lines) connect the sarcomeres together along the myofibril. It is a complex structure of proteins in which actin filaments and titin are anchored. In a relatively recent review, Frank and Frey (2011) underline the strategic position of the Z-disk “to sense, integrate, and transduce biomechanical stress signals”, and present an overview of their putative role in the development of severe cardiomyopathies, see also (Wadmore, Azad, and Gehmlich 2021).
- M-lines connect the thick filaments in the hexagonal lattice transverse to the direction of the fibrils. Their role in the contraction mechanics has been reviewed by Lange et al. (2019). The authors argue that the M-lines “stabilize” the active fibrils by limiting the misalignment of the thick filaments while they exert force, see also (Agarkova et al. 2003; Schoenauer et al. 2005).
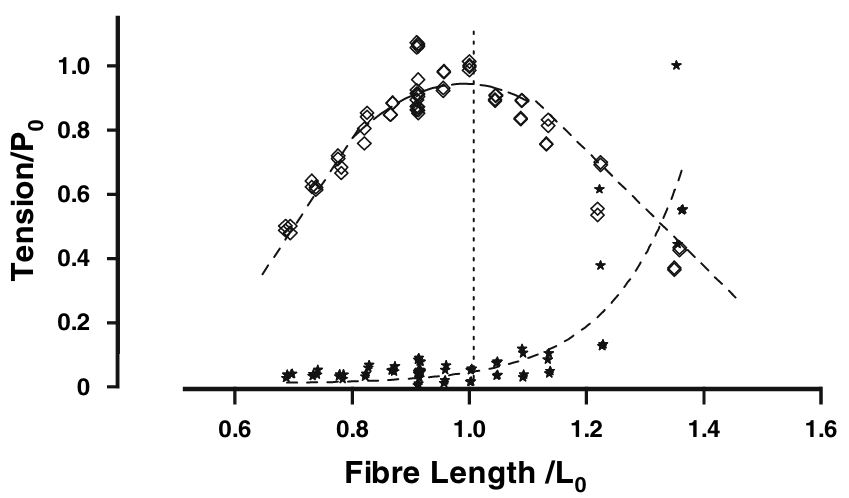
- Titin is the largest protein in the human genome. It connects the two Z-lines of a sarcomere and runs along the thick filament. When the muscle is relaxed, there are no cross-bridges linking the actin and myosin filament and therefore, in the absence of titin, there would be no structure, appart from the fibers’ membrane themselves, preventing the sarcomeres from over stretching, as the filament would slide freely. This “safeguard” function was supported by numerous passive mechanial tests showing a non-linear hyperelastic behavior, with a strong “enthalpic” stiffening at large elongations, see Figure 5.5. In the next section, we will explain its central role in the regulation of the contraction.
5.1.3 Three-filament theory of contraction
In view of the classical fiber mechanical measurements (Figure 5.5), it seemed that near physiological regimes, titin would work mostly in an “entropic” regime with negligible contribution to the total force. The physiological role of titin has been completely reconsidered in the past decade, in particular thanks to the work of W. Herzog and colleagues to which the terminology “three-filament theory” (actin-myosin-titin) can be attributed (Schappacher-Tilp et al. 2015). In short, titin is sensitive to calcium ions and, as such, its properties in the passive and active regimes are in fact completely different.
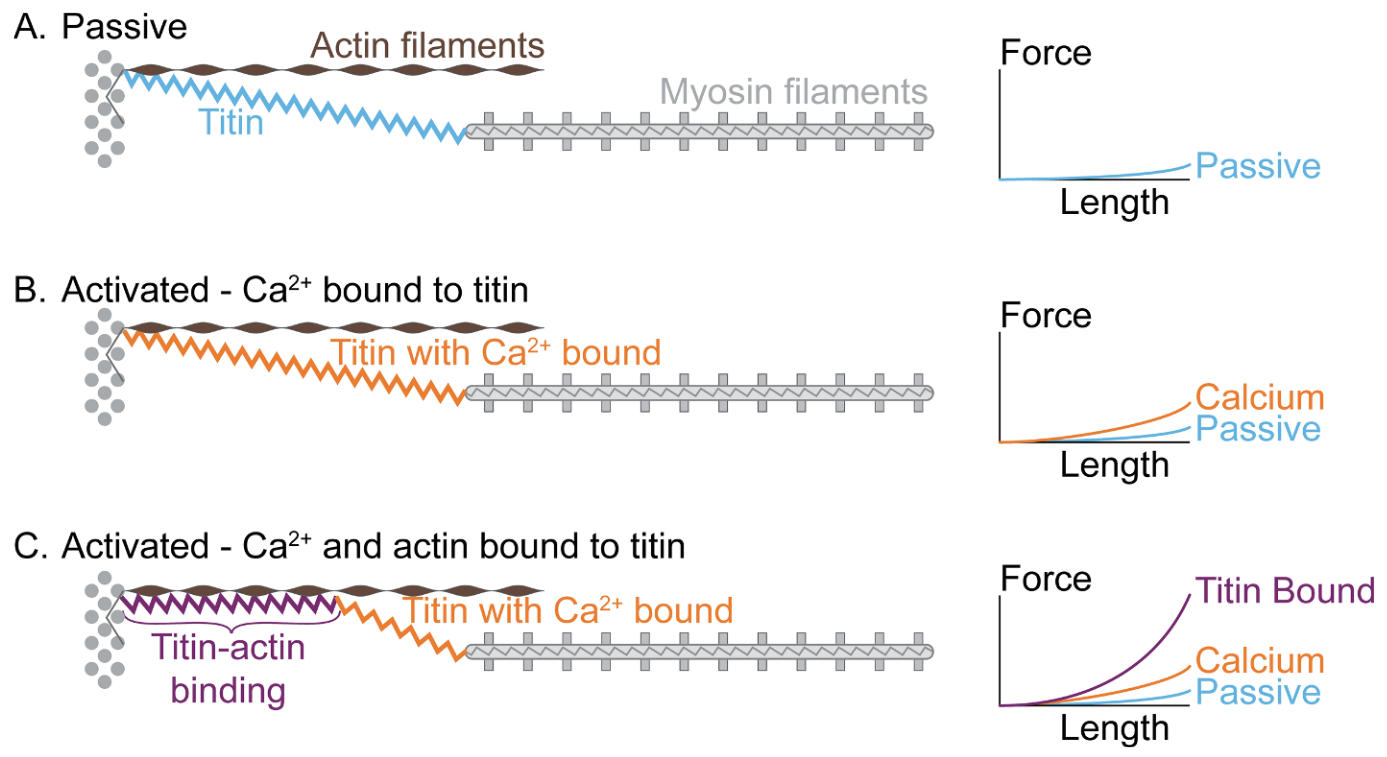
The active contraction model involving titin is summarized in Figure 5.6. In the passive regime (A), the classical behavior is observed, with a very low stiffness at physiological sarcomere elongation. This low entropic stiffness is due to the PEVK domains of the molecule that unfold under tension. Upon activation and before the onset of actin-myosin interaction this stiffness slightly increases (Powers et al. 2014). When actin and myosin start to interac, titin proximal N2A calcium sensituve domain binds to actin, which result in drastic reduction of the titin’s length and thereby a 100-fold increase of its stiffness (Powers et al. 2020). We refer to the review by Herzog and Schappacher-Tilp (2023) for further references on the experimental measurements.
Based on the experimental observations, the mechanical model suggested by Ford, Huxley, and Simmons (1981) (see Figure 4.3) has been revisited by Pertici, Caremani, and Reconditi (2019) to incorporate the contribution of titin. The results confirm numerous previous studies showing that the original model of Ford, Huxley, and Simmons (1981) was inaccurate only at low force, which corresponds to the begining of the contraction or to contraction at near maximal velocities (Brunello et al. 2006).
5.1.4 Contraction regulation mechanisms
We here provide a short presentation of the physiological mechanisms controling the level of activation of the contractile machinery. The interested reader can find a more thorough up-to-date presentation with an extended list of reference in the recent review by Brunello and Fusi (2024). We also refer to the introduction of Kimmig (2019) and Kimmig, Caruel, and Chapelle (2022).
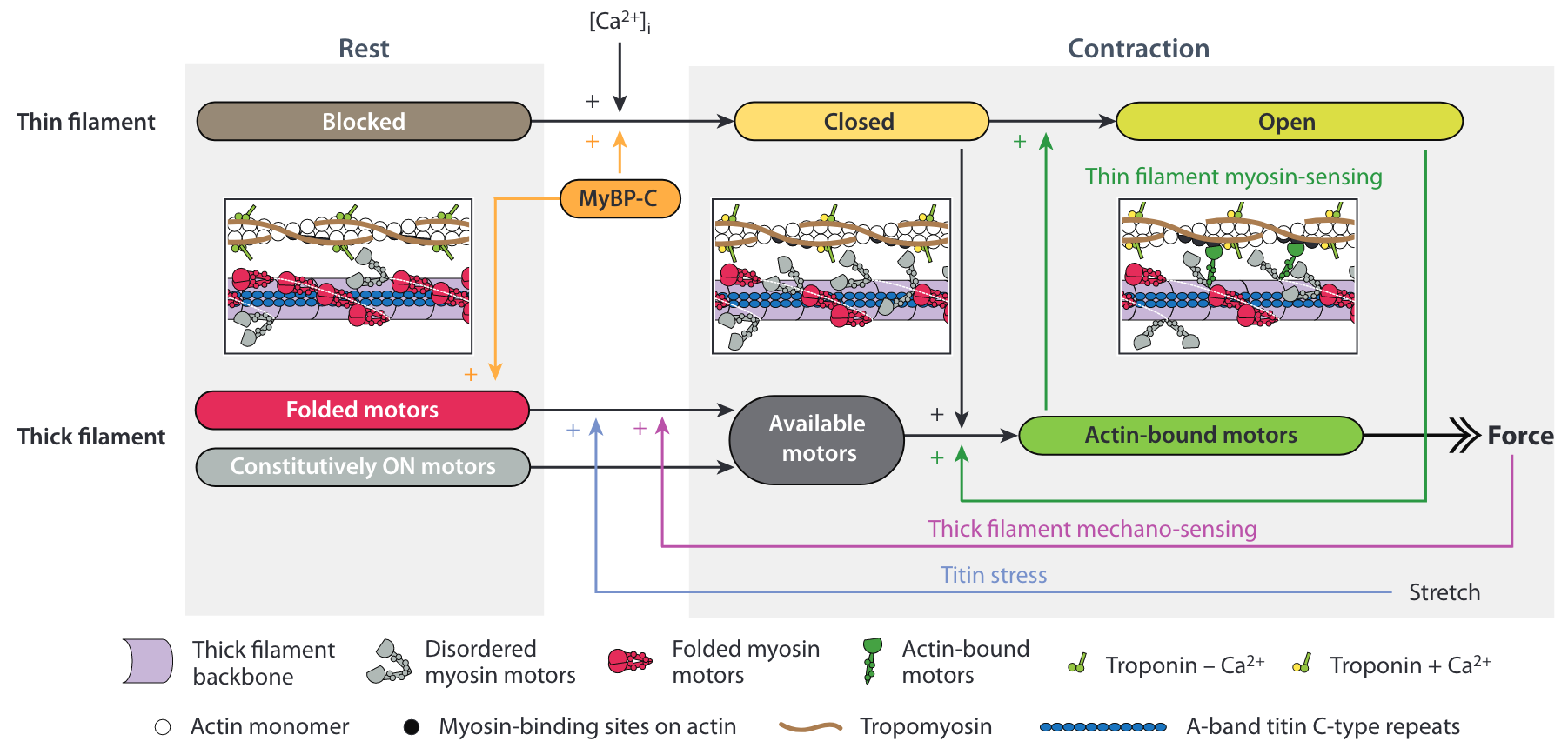
The contraction is activated by the release of calcium ions in the cytoplasm of the muscle cells, see the top row of Figure 5.7. The concensual mechanism is that the calcium ions (Ca2+) bind to the regulatory units formed by the Troponin-Tropomyosin complexes that are coiled around the actin filament (McKillop and Geeves 1993). In the relaxed state these complex “cover” the actin binding sites, which prevents myosin attachment (blocked state). The binding of Ca2+ to a regulatory unit induce a conformational change that partially reveal the binding site (closed state) and alow weak myosin binding. The binding of a myosin “locks” the regulatory unit and the attachment become strong (open state).
In the last decade, it became clear that there is also an activation mechanism associated with the thick filament, which is particularly important for heart contraction, see the bottom row of Figure 5.7. In the relaxed state, the myosin motors are is a so-called OFF-state: the majority of the myosin heads are in an autoinhibitory conformation [called the Interacting Head Motif, IHM, see (Woodhead and Craig 2020)] folded back on the thick filament. The thick filament activation is not directly due to calcium. It results from a positive force feedback transmitted by the thick filament itself and by the titin protein,2 which triggers the transition of the myosin motor from the OFF-state to the ON-state (Linari et al. 2015; Reconditi et al. 2017; Squarci et al. 2023).
2 We recall that titin runs along the thick filament, and gets stiffer upon activation.
Numerous experimental results also support the idea that there is a cooperative mechanism at work in the actin filament as well (green vertical arrow in Figure 5.7). The principle of this mechanism is that force generating myosin motors may propagate the regulatory unit conformational change without the need for extra calcium ions (Caremani et al. 2022). Hence, the strong binding of a myosin motor can facilitate the binding of neighboring motors.
These recent observations clearly show that the single motor description is sufficient to take into account these cooperative activation mechanisms. They also put the long-range mechanical feedback loop mediated by the cytoskeletal structural protein like titin at the center of the picture.
5.1.5 Non-affine deformation along muscle fibrils
Over the past two decades, experimental studies at the scale of single fibrils comprising a few sarcomeres have revealed the existence of non-uniformities (non-affine behavior) of the sarcomere lengths during contraction (Li et al. 2023; Moo and Herzog 2018). A recent review of these studies reports on the important role played by the elastic network that connects the contractile units together in tailoring these non-uniformities and in determining the force production (Leite and Rassier 2020). As mentioned in Section 1.4.3, these non-uniformities may play a significant role in the development of severe cardiomyopathies. One problem is that there is no experimental setup available to monitor individual contractile unit. Individual sarcomere lengths can however be monitored (Li et al. 2023; Lookin, Khokhlova, and Cazorla 2022; Moo and Herzog 2018). Another issue is that little is known about the elastic properties of the Z and M-lines, so the calibration of these elements might be difficult.
We recall that one of the hypotheses usually made to formulate models of muscle contraction is that fibers can be modelled as a uniform continuum, see Section 2.1.3. This hypothesis implies an affine deformation of the fiber, which is not in accordance with the potential onset of sarcomere length non-uniformities. Hence, reconsidering the modeling of muscle fibers in a multiscale framework would be necessary to capture potential effect of cardiomyopathies affecting the mechanical properties of cytoskeletal proteins.
5.1.6 Fiber orientations in the muscle tissue
A second hypothesis shared by macroscopic models of muscle contraction is that a single fiber orientation can be defined at each material point, see Figure 2.2. Figure 5.8 shows micrographs of cardiac tissue illustrating the orientation of fibers in a normal adult heart (A), a hypertensive heart (B) and in a heart with hypertrophic cardiomyopathy (C). It is clear that in the latter case the definition of a unique fiber orientation is not possible, at least in this sample.
Tueni, Allain, and Genet (2023) proposed a multiscale model of the passive myocardium using different representations of the microscopic organisation of cardiomyocites within the extracellular matrix, see also (Avazmohammadi et al. 2017). The objective of this study is to determine which type of microstructure best reproduces the observed anisotropic passive response of tissue samples (Dokos et al. 2002; Sommer et al. 2015). Such study could be extended considering the active mechanisms, in particular activation.
5.2 Challenges
The above developments of mesostructures based models are so far adressing only the passive behavior of the tissue, so they remain to be coupled to active rheological laws. Furthermore, our previous work on the collecive behavior of molecular motors within a single contractile unit (see Chapter 4) has revealed the consequences of long-range elastic interactions exsiting between them. In particular, it has been shown that these interactions could lead to finite size collective effects like synchronized working strokes (Caruel, Allain, and Truskinovsky 2013; Caruel and Truskinovsky 2018), that usual mean-field model cannot capture. These findings are compatible with the presence of non-affine deformation at the mesoscale, with for instance some contractile units being in one conformation while others being in another conformation, see Section 5.3.1. Such non-affine deformation are observed at the fibril scale, so understanding the mechanisms underpinning the onset of these inhomogeneities may be of importance for medical applications.
Another question is to find an adequate model of the regulations mechanisms. The role played by the cytoskeleton on these mechanisms might reveal to be the major determinant of the inter-sarcomere dynamics (Leite and Rassier 2020). Finding a path towards a meaningful mesoscale model of muscle contraction activation and regulation is difficult because there is still no consensus on the underlying physiological mechanisms.
All these issues may lead to reconsidering the classical rheological representation presented in Section 2.1.3.
5.3 Contributions
5.3.1 Passive behavior of a simplified sarcomere chain
The following results are presented in more details in (Caruel and Truskinovsky 2018, sec. 2.3)
To follow on the results presented in (Caruel, Allain, and Truskinovsky 2013) and (Caruel and Truskinovsky 2017), Caruel and Truskinovsky (2018) presented preliminary results on a statistical mechanical model of two antagonists contractile units and then of a chain of contractiles units. This work concerns only the coordination of power-stroke conformational changes with the same fixed number of myosin motors in each contractile unit. Hence, the study does not include the attachment-detachment side of the actin-myosin interaction and should thus be considered only in the context of the short timescale response to fast load changes.
We recall that the equilibrium tension-elongation relation of a single contractile unit depends on the loading device, see Section 4.3.5. In a hard device, the response can show a region of negative stiffness, while, at similar temperature, the soft device response is characterized by a plateau, see Figure 4.7 and associated discussion. In the post bifurcation regime (low temperature or low backbone stiffness, see phase III in Figure 4.7), the assembly of cross-bridges tends to behave synchronously: the vast majority of the proteins adopting the same conformation at any given time. The consequence of this property is that the deformation can differ from one contractile unit to the next. With such a behavior, one can expect the deformation associated with muscle contraction to be globally non-affine.
In (Caruel and Truskinovsky 2018), this intuition was confirmed by computing the equilibrium response, at zero and finite temperature, of two or more contractile units in series. Interestingly, the equilrium deformation in a hard device (imposed length) is non-affine which confirms previous numerical and experimental studies (Vilfan and Duke 2003; Shimamoto et al. 2009; Leite and Rassier 2020). In contrary, in a soft device (imposed force), the systems never explores non-affine states.
Comparing the derived non-affine tension-elongation relations with those calculated under the premise that each contracile unit acts as a basic constitutive element with a predetermined tension-elongation relation is enlightening. To do so, we assume that the “constitutive” tension-elongation relation corresponds either to the soft or the hard device equilibrium response of a single contractile unit.
The single sarcomere responses obtained by combining such “phenomenological” units in series in hard and soft device loadings are shown in Figure 5.9. The thick lines show the thermal equilibrium tension-elongation relation computed exactly (using full ensemble averaging). The thin lines are obtained by assuming the constitutive relations.
If the chosen constitutive relation corresponds to that obtained following a hard device protocol [see (a) and (c)], we obtain several equilibrium states for a given total elongation, which is directly imposed by the non-convexity of the constitutive constraints. The global minimum path predicted by the “constitutive model” (thin lines) shows discontinuous transitions between stable branches which resemble continuous transitions along the actual hard device thermal equilibrium path, see the thick line in (a). If instead we use the soft device constitutive law for the description of individual half-sarcomeres [see (b) and (d), thin lines], the tension-elongation response becomes monotone and is therefore completely unrealistic regarding the hard-device thermal equilibrium path (thick lines), see (b). It is however fit to the equilibrium response in a soft device, see (d).
These preliminary results show that the challenge in developing a macroscopic continuum theory for skeletal muscles arises from the model producing different constitutive relations for soft and hard devices, and the possibility that mixed loading conditions could lead to other relations. This complexity suggests that a local constitutive approach might not be sufficient for a medium governed by long-range interactions. Instead, it may be necessary to explore a nonlocal constitutive closure for the balance law system.
5.3.2 Coupling actin-myosin interaction mechanics and contraction regulation processes
The work summarized in this section has been published by Kimmig, Caruel, and Chapelle (2022).
Numerous phenomenological models have been developed to investigate the interplay between force production anf the thick and thin filament activation processes, see Trayanova and Rice (2011) for a review and Regazzoni, Dedè, and Quarteroni (2020) for a more recent contributions.3 These models have the common characteristic of not taking into account the relative sliding of actin and myosin filaments and its effect on the population densities occupying the different states. This effect may in fact play a major role in the regulation process, specially in the case of cardiac contraction.
3 The approach proposed by Regazzoni, Dedè, and Quarteroni (2020) shows similarites with the one presented here, see the introduction of (Kimmig, Caruel, and Chapelle 2022) for more explanations of the differences.
Kimmig, Caruel, and Chapelle (2022) recently worked on setting the framework for combining the two modeling aspects regarding the thin filament activation process. This work is the follow-up of a paper by Kimmig, Moireau, and Chapelle (2021) on the length dependent force generation, which was focusing on the thick filament regulation mechanisms.
The modeling framework is summarized in Figure 5.10. Within a sarcomere (a), models can be formulated to describe the interaction between myosin proteins and their neighboring actin filaments (b). For this interaction to take place, both myosin motors and actin binding sites needs to be active, see (Brunello and Fusi 2024). In the intactive state (OFF-state, 0), myosin motors are folded back on the thick filament and cannot interact with actin, see Figure 5.10 (e). Active motors (ON-state, 1) can attach only to an actin site that has been activated by the binding of a calcium ion to troponin, see state P in Figure 5.10 (f).
In the proposed model, the actin site is a unit that can exist in four different states depending on wether it is activated or not (N or P) and wether it is occupied by a myosin head or not (0 or 1). Kimmig, Caruel, and Chapelle (2022) show how the conservation law for the populations of these four sates can be coupled to the attachment-detachment process of myosin heads, within the framework of the classical Huxley-Hill two-state model (see Section 3.2.1).
In this model, the internal variable \(\gamma\in\{0,1\}\) represent two pools of myosin heads, the value 0 (repectively 1) being associated to heads that are not available (respectively available) for attachment. The fraction of heads that are available is denoted by \(n_0\). We denote by \(P_{1}(s,t,\gamma)\), the probability for a head pertaining to the pool \(\gamma\), that is located at a distance \(s\) from its nearest binding site to be attached at time \(t\).
We recall that in the classica Huxley-Hille model, the conservation for \(P_{1}(s,t)\) reads (see Equation 3.1) \[ \partial_t P_{1}(t,s) + \dot{x}_{c}(t) \partial_s P_{1}(t,s) =-g(s) P_{1}(t,s) + f(s) \left[1 - P_{1}(t,s)\right] \]
For a subset of heads located at a distance \(s\) from their nearest binding site, the state of the thin filament can be described by
- \(n_a\) the ratio of activated actin site, which is considered as a prescribed parameter in (Kimmig, Caruel, and Chapelle 2022)
- \(\overline{n}_a(s,t,\gamma)\) the ratio of activated actin site occupied by a bound myosin head.
In the model proposed by Kimmig, Caruel, and Chapelle (2022), the attachement and detachment rates depend on the state of the actin site (\(na\), \(a\): non activated or activated, respectively), and the availability of the myosin head \(\gamma\). The rates corresponding to the different transitions of the four-state model shown in Figure 5.10 are then denoted by \(f_{\gamma,\text{a}}\) and \(f_{\gamma,\text{na}}\) for attachments, and \(g_{\gamma,\text{a}}\) and \(g_{\gamma,\text{na}}\) for detachments. Notice that, attachments to a non activated site, or of an unavailable head is by design possible, to preserve mathematical consistency, but the calibration will ensure that the corresponding rates will be low.
Using these quantities, the dynamics of \(P_{1}\) and \(\overline{n}_a\) can be written as4 \[ \left\{ \begin{aligned} &\begin{split} \dfrac{\mathrm{d}}{\mathrm{d}t} P_{1}(s,t, \gamma) & = f_{\gamma,\text{a}} \overline{n}_a+ f_{\gamma,\text{na}} \big( 1 - P_{1} - \overline{n}_a\big) \\&\quad- g_{\gamma,\text{a}} \big( n_a- \overline{n}_a\big) - g_{\gamma,\text{na}} \big(\overline{n}_a- n_a+ P_{1}\big), \end{split}\\ &\begin{split} \dfrac{\mathrm{d}}{\mathrm{d}t} \overline{n}_a(s,t, \gamma) & = \dfrac{\vert \dot{n}_a \vert_{+}}{1 - n_a} \big(1 - P_{1} - \overline{n}_a\big) + g_{\gamma,\text{a}} \big( n_a- \overline{n}_a\big) \\&\quad- \dfrac{\vert \dot{n}_a \vert_{-}}{n_a} \overline{n}_a- f_{\gamma,\text{a}} \overline{n}_a, \end{split} \end{aligned} \right. \tag{5.1}\]
4 The details of the computations leading to this sytem can be found in (Kimmig, Caruel, and Chapelle 2022, sec. 2.2.2 and 2.2.3). We use the notations \[ \begin{aligned} \vert x \vert_{+} &= \begin{cases} x, & \text{if } x \geq 0, \\ 0, & \text{otherwise}, \end{cases} \\ \vert x \vert_{-} &= \begin{cases} - x, & \text{if } x \leq 0, \\ 0, & \text{otherwise}. \end{cases} \end{aligned} \]
where, the total time derivatives are defined by \[ \begin{aligned} \dfrac{\mathrm{d}}{\mathrm{d}t} P_{1}(s,t,1) & = \partial_{t}\, P_{1}(s,t,1) + \dot{x}_c\, \partial_{s} P_{1}(s,t,1) + \dfrac{\vert \dot{n}_0 \vert_{+}}{n_0} \Big[ P_{1}(s,t,1) - P_{1}(s,t,0) \Big], \\ \dfrac{\mathrm{d}}{\mathrm{d}t} \overline{n}_a(s,t, 1) & = \partial_{t}\, \overline{n}_a(s,t, 1) - \dot{x}_c\, \partial_{s}\, \overline{n}_a(s,t, 1) + \dfrac{\vert \dot{n}_0 \vert_{+}}{n_0} \Big[ \overline{n}_a(s,t,1) - \overline{n}_a(s,t,0) \Big]. \end{aligned} \]
The model dynamics given by Equation 5.1 was calibrated in Kimmig, Caruel, and Chapelle (2022) based on experimental data obtained from isometric twitch contractions of cardiac trabeculae [Kentish et al. (1986); Janssen and Hunter (1995); Dobesh, Konhilas, and Tombe (2002); ter Keurs et al. (2008); Caremani et al. (2016);].
We postulate that \(n_a(e_{c}, t, C) = n_{a,\infty}(e_{c}, C) n_{a,t}(e_{c}, t)\). The function \(n_{a,\infty}\) accounts the variations of steady-state level of activation with the sarcomere extension \(e_{c}\), and a level of calcium supply parameter \(C\) that accounts for the contractility. The function \(n_{a,t}\) describes the time transients.
At this stage, both functions \(n_{a,\infty}\) and \(C\) are fitted manually on data from various publications, which makes the model purely phenomenological, and thus not based on a physical description of the activation process per se. The main result of (Kimmig, Caruel, and Chapelle 2022) is to set the framework where a physical model of activation can be coupled to a Huxley-Hill-like actin-myosin interaction model.
5.4 Perspectives
5.4.1 Anatomic structures
As we mentioned in Section 1.1.1, the muscle tissue has a hierarchical structure decomposed from the macroscale to the nanoscale as tissue, fascicles, fibers, fibrils, sarcomeres, contractile units, molecular motors. We termed “mesoscale”, structure ranging from the sarcomeres to fibers which is already containing three hierarchical levels. This chapter showed our contributions to the lowest levels of this hierarchy. To improve our current understanding of the multiscale mechanics of the muscle tissue in health and disease, emphasis has to be put on - the connective structure between sarcomeres in a more realistic model of a non-homogenous fiber, - the organisation of fibers within the extracellular matrix, which implies to reconsider the macroscopic model where, so far, only a single direction per material point is considered.
5.4.2 Modeling activation
Our understanding of the muscle contraction regulation mechanisms has made a considerable leap forwards over the past five years, see Section 5.1.4. The discovery of long-range cooperative mechanisms will necessarily result in the development of models of interacting contractile units where cytoskeletal proteins (titin, Z-lines, M-lines) will play a central role.